55501328
Geometrie – Trapez
In unserem Arbeitsheft Mathematik 10, Vol. 1 – Geometrie – Trapez finden Sie 50 interaktive und didaktisch aufbereitete Aufgaben.
Das Medium bietet H5P-Aufgaben an, die ohne zusätzliche Software verwendbar sind. Das Medium enthält 25 H5P-Aufgaben zum Thema Mathematik.
Durch interaktive Aufgabentypen wird das audiovisuelle und interaktive Lernen einfach.
Lernen macht jetzt Spaß!
Included Tasks
- 1. Symmetrisches Trapez - Flächeninhalt - 5 interaktive Aufgaben (1)
- 2. Symmetrisches Trapez - Flächeninhalt - 5 interaktive Aufgaben (2)
- 3. Symmetrisches Trapez - Flächeninhalt - 5 interaktive Aufgaben (3)
- 4. Symmetrisches Trapez - Flächeninhalt - 5 interaktive Aufgaben (4)
- 5. Symmetrisches Trapez - Flächeninhalt berechnen (h fehlt) (1)
- 6. Symmetrisches Trapez - Flächeninhalt berechnen (h fehlt) (2)
- 7. Symmetrisches Trapez - Flächeninhalt berechnen (h fehlt) (3)
- 8. Symmetrisches Trapez - Flächeninhalt berechnen (h fehlt) (4)
- 9. Symmetrisches Trapez - Höhe berechnen (Winkel fehlen) (1)
- 10. Symmetrisches Trapez - Höhe berechnen (Winkel fehlen) (2)
- 11. Symmetrisches Trapez - Höhe berechnen (Winkel fehlen) (3)
- 12. Symmetrisches Trapez - Höhe berechnen (Winkel/Formeln fehlen) (1)
- 13. Symmetrisches Trapez - Höhe berechnen (Winkel/Formeln fehlen) (2)
- 14. Symmetrisches Trapez - Höhe berechnen (Winkel/Formeln fehlen) (3)
- 15. Symmetrisches Trapez - Winkel cos(beta) berechnen (1)
- 16. Symmetrisches Trapez - Winkel cos(beta) berechnen (2)
- 17. Symmetrisches Trapez - Winkel cos(beta) berechnen (3)
- 18. Symmetrisches Trapez - Winkel cos(gamma) berechnen (1)
- 19. Symmetrisches Trapez - Winkel cos(gamma) berechnen (2)
- 20. Symmetrisches Trapez - Winkel cos(gamma) berechnen (3)
- 21. Symmetrisches Trapez - Diagonale (e) - 5 interaktive Aufgaben (1)
- 22. Symmetrisches Trapez - Diagonale (e) - 5 interaktive Aufgaben (2)
- 23. Symmetrisches Trapez - Diagonale (e) - 5 interaktive Aufgaben (3)
- 24. Symmetrisches Trapez - Winkel berechnen (1)**
- 25. Symmetrisches Trapez - Winkel berechnen (2)**
- 26. Symmetrisches Trapez - Winkel berechnen (3)**
- 27. Symmetrisches Trapez - 5 gemischte Aufgaben (mit Formeln) (1) *
- 28. Symmetrisches Trapez - 5 gemischte Aufgaben (mit Formeln) (2) *
- 29. Symmetrisches Trapez - 5 gemischte Aufgaben (mit Formeln) (3) *
- 30. Symmetrisches Trapez - 5 gemischte Aufgaben (mit Formeln) (4) *
- 31. Symmetrisches Trapez - 5 gemischte Aufgaben (mit Formeln) (5) *
- 32. Symmetrisches Trapez - 5 gemischte Aufgaben (mit Formeln) (6) *
- 33. Symmetrisches Trapez - 5 gemischte Aufgaben (mit Formeln) (7) *
- 34. Symmetrisches Trapez - 5 gemischte Aufgaben (mit Formeln) (8) *
- 35. Symmetrisches Trapez - 5 gemischte Aufgaben (mit Formeln) (9) *
- 36. Symmetrisches Trapez - 5 gemischte Aufgaben (mit Formeln) (10) *
- 37. Ordne das passende Trapez den Abmessungen zu! (1)
- 38. Ordne das passende Trapez den Abmessungen zu! (2)
- 39. Ordne das passende Trapez den Abmessungen zu! (3)
- 40. Ordne das passende Trapez den Abmessungen zu! (4)
- 41. Symmetrisches Trapez - 5 gemischte Aufgaben (ohne Formeln) (1) **
- 42. Symmetrisches Trapez - 5 gemischte Aufgaben (ohne Formeln) (2) **
- 43. Symmetrisches Trapez - 5 gemischte Aufgaben (ohne Formeln) (3) **
- 44. Symmetrisches Trapez - 5 gemischte Aufgaben (ohne Formeln) (4) **
- 45. Symmetrisches Trapez - 5 gemischte Aufgaben (ohne Formeln) (5) **
- 46. Symmetrisches Trapez - 5 gemischte Aufgaben (ohne Formeln) (6) **
- 47. Symmetrisches Trapez - 5 gemischte Aufgaben (ohne Formeln) (7) **
- 48. Symmetrisches Trapez - 5 gemischte Aufgaben (ohne Formeln) (8) **
- 49. Symmetrisches Trapez - 5 gemischte Aufgaben (ohne Formeln) (9) **
- 50. Symmetrisches Trapez - 5 gemischte Aufgaben (ohne Formeln) (10) **
Curriculum-centred and oriented towards educational standards
Matching
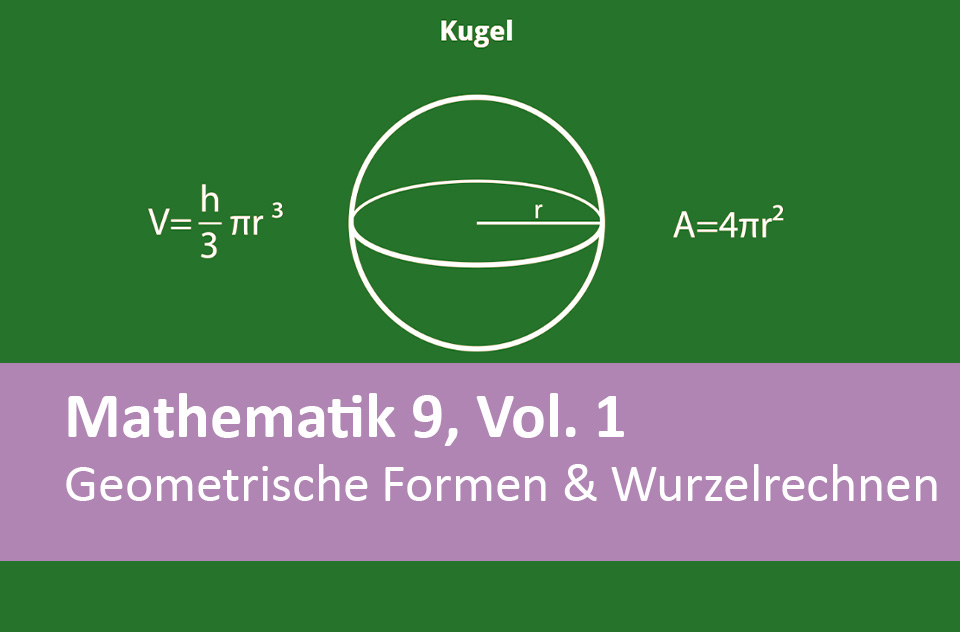
Geometrische Formen & Wurzelrechnen
In unserem Arbeitsheft Mathematik 9 – Geometrische Formen & Wurzelrechnen finden Sie 50 interaktive und didaktisch aufbereitete Aufgaben.
Units of Length
The DVD starts with a look back into the past. How did peop- le measure in former times? What historical units of measure- ment were there? What is the standard metre? Since when has there been a system of units? Subsequently, the units of measurement – metre (m), centimetre (cm), milllimetre (mm), decimetre (dm) and kilo- metre (km) – are examined more closely. In a third chapter, an overview of the conversions is presented and their systematics explained. Decimal points and the prefixes are clearly illustrated. Then the DVD offers a digression visiting other countries and their length units. America and Great Britain, with inches, feet, yards and miles, play a central role. In the fifth chapter, calculations using scales are presented. Here the focus is laid on scales in maps, but also scaling down and up are dealt with. In the last chapter, circumferences of rectangles and squares are measured and calculated with various examples.
Rechenspurgeschichten
Ob im Weltraum, auf dem Bauernhof oder im Märchenland … wo auch immer sie hinkommen, werden Lisa, Tim und Mia vor Aufgaben zu den Grundrechenarten gestellt.